|
Stick-Ken
Stick-Ken
is a Sudoku-like puzzle where you fill a grid with the digits 1–9 (for
a 9x9 Kendoku) so that each row and column has all digits once and only
once.
In
addition, each shape within the grid must fulfill the arithmetic result
given for that shape. Individual shapes may contain a digit
twice, but within each row and column a digit can be used only once.
The four arithmetic operations used are Addition (+),Subtraction (-), Multiplication ( ), and Division (�).
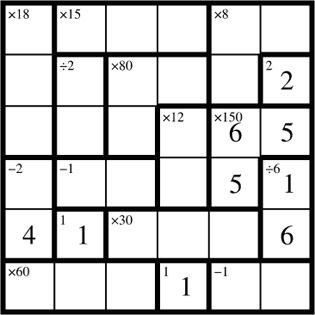
A sample 6x6 Kendoku is given here. In a 6x6 Kendoku, you need to use the digits 1–6.
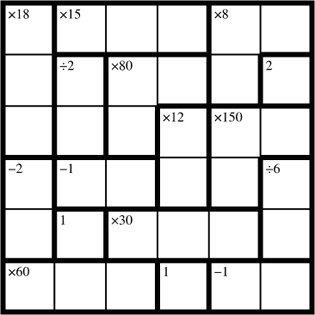
Solving a Puzzle:
The
clues in single-box shapes are direct values for that box. Fill them in
first. For example, in the 6x6 grid below, the fourth cell in the
bottom row and the second cell in the fifth row are single-box shapes.
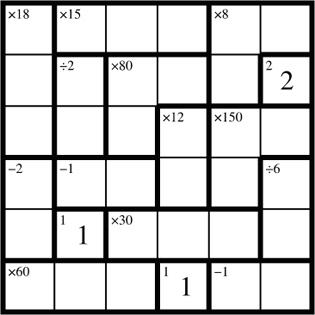
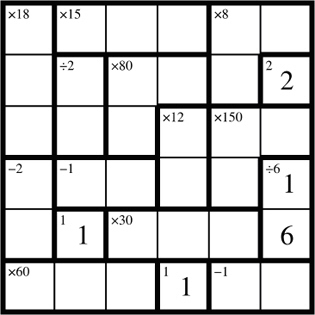
Next,
try to find possibilities for a small shape. The �6 shape in the
last column has only one possible combination of numbers (i.e. 1 and
6). Given that a number 1 is already found in the fifth row (in
the second column), the number 1 that fits this equation can only go in
the fourth row, leaving the number 6 to go in the fifth row.
People
get intimidated by the fact that a shape may have a digit twice.
But that sometimes helps us solve the puzzle quicker.
For
example, the 150 in the last two columns can have only one
possible combination of numbers (i.e. 6 5
5). Given that 5 is used twice, and that the 5 has to be in
different rows and different columns, there is only one way to place
these three numbers. The 6 goes in the third row, fifth column, and 5s
go in the other cells.
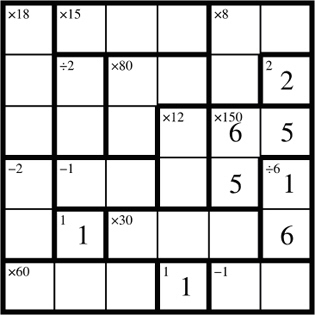
In
the fifth row, 30 has two possible number combinations:
1 6 5 or 2 3 5.
Given that 1 and 6 are already used in this row, we can eliminate that
possibility. This means that we have to use 2 3
5. Although we don’t know which digit goes where, this does leave
the first column of the fifth row with only one remaining possibility—4.
The
8 in the first two rows (last two columns) has only one possible
combination: 1 2 4. Given that digits 1
and 2 are already used in the last column, the cell on the top row,
last column must be 4. The fifth cell in the top row must be 2
(because 2 is already used in the second row and cannot be
repeated). The remaining cell in the second row, fifth column is
therefore 1.
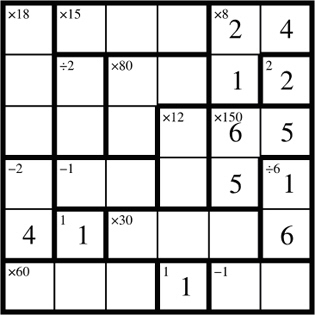
Now you can solve the rest of the puzzle using similar techniques. The solution for this example is:

|